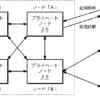
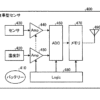
インターネットを利用しているとしばしば「暗号化」という言葉を目にします。「暗号化」は、大事な情報を第三者に盗み見られないようにするための技術です。
暗号は、簡単に解読されるようではいけません。暗号の解読が難しいのは、大きな数の素因数分解が難しいことと関係しているんです。以下で解説します。
大事な情報が通信中に盗み見られないようにするための暗号化技術
インターネットを利用しているとしばしば「暗号化」という言葉を目にします。「暗号化」は、大事な情報が通信によって相手に運ばれている途中に他人に盗み見られないようにするための技術です。大事な情報を保存しておくときに、他人に盗み見られないようにするためにも使われます。
インターネットを介した情報のやりとりで、誰かに盗み見されるのを防ぐために暗号化が行われている、という漠然としたイメージはつく方も多いことでしょう。このイメージは正しいのですが、そもそもこの暗号化がどのように行われているのか、暗号化のしくみをあなたはご存知でしょうか?
暗号化のしくみのヒントは素因数分解
このヒントとなるのは「素因数分解」です。誰もが中学・高校時代の数学の授業で経験し、もしかしたら言葉すら聞きたくないほど大嫌いな方もいらっしゃるかもしれません。
まず、素数というのは、1と自分自身でしか割り切れない数のことをいいます。小さい方からいくと、2,3,5等があります。現段階では、素数は、無限にあることが知られています。
次に、素因数分解というのは、数を、素数(1とその数自身以外で割り切れない数)の積に分解して表現することです。例えば、72は、23×32というように、素数2と素数3の積に分解して表現されます。積の形に表現したときの1つ1つの数を因数というので、素因数分解というのは、ある数を、素数の因数に分解することと言えます。
- 72=2×2×2×3×3=23×32
別の例では、121は、112というように、素数11の積に分解して表現されます。
- 121=11×11=112
このように、72とか121というような比較的小さな数の素因数分解は、簡単で、答えもよく知られています。でも、大きな数の素因数分解は、簡単ではありません。
大きな数が素数かどうか判断するのは難しい 大きな数の素因数分解も難しい
大きな数が、素数なのかどうか、また、どんな素数の積で表現できるかを判断するのは難しいのです。
例えば78457591が素数なのか、素数でないのかを判断することは難しいのです。
素数でない場合は、素因数分解できるはずなのですが、どの素数の積なのかを判断するのも難しいです。これは、人間の頭でも難しいのですが、コンピュータにとっても難しい問題です。
- 78457591は素数?
- 78457591= 〇 × 〇?
(ちなみに、78457591は、素数ではなく、素数9973と素数7867の積です。)
1つの素数が分かれば、もう1つは簡単にわかる
一方で、2つの素数の積である数の片方の素因数がわかっていれば、もう1つの素因数は簡単に分かります。割り算をするだけです。例えば、78457591の素因数の1つが9973であるとわかれば、もう1つの素因数は7867とすぐにわかります。
- 78457591÷9973=7867
大きな数でもコンピュータは高速にもう一方の素因数を求めることができます。この原理を利用したのが、暗号化の理論です。
暗号化した情報と、「鍵」があれば、もとの情報が分かる
コンピュータは、文書でも画像でも音声でも、全ての情報を数値(正確には二進数)として処理しています。
ある情報となる数値に大きな数を用いて何らかの演算を施したものについては、何の情報もない状態ではコンピュータを用いても、処理される前の情報を掘り起こすことは難しいです。反対に、事前に情報が与えられていれば、処理される前の目的の情報に即座にたどり着けます。
このように、情報を掘り起こすことが困難であることを利用したのが暗号化です。第三者が悪意をもって、データを盗み見しようにも、暗号化に際して使われる数である「暗号鍵」を知らない第三者は暗号文を解読できません。この性質を利用して、鍵を持つ者同士で情報のやりとりができるのです。
暗号化の原理については少々難解なので割愛しますが、その基礎には先に説明したような素因数分解があります。興味のある方は「RSA暗号」という言葉を調べてみて下さい。
今日のみどころ
通信の暗号化が素因数分解の性質と関係していることを解説しました。学校で勉強したことがしっかり現代の情報社会を支えてくれている良い例です。こうやって役に立っているんだよと教えてあげたいですね。
暗号化に関する技術について興味がある方は、こちらもチェックしてみてください。